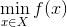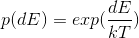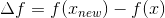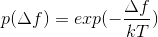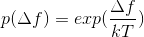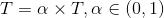模拟退火算法--Intelligent technology investment network-上海优钧机械设备科技

News Message

模拟退火算法

by show 2021-02-15

模拟退火算法

在实际日常中，人们会经常遇到如下问题：在某个给定的定义域内，求函数对应的最优值。此处以最小值问题举例（最大值问题可以等价转化成最小值问题），形式化为：
$\min_{x \in X}f(x)$
如果是离散有限取值，那么可以通过穷取法获得问题的最优解；如果连续，但是凸的，那可以通过梯度下降等方法获得最优解；如果连续且非凸，虽说根据已有的近似求解法能够找到问题解，可解是否是最优的还有待考量，很多时候若初始值选择的不好，非常容易陷入局部最优值。
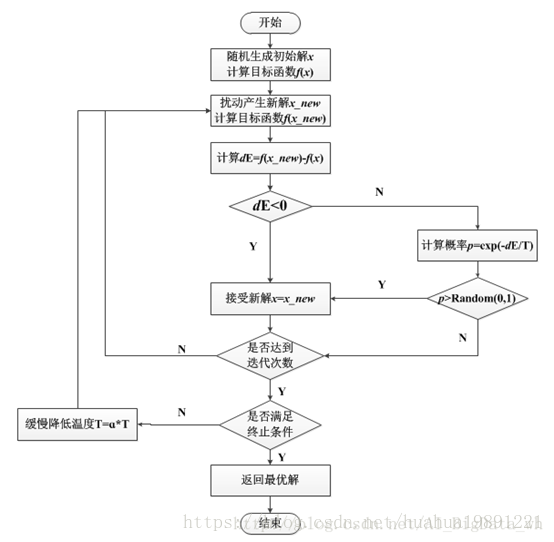
随着日常业务场景的复杂化，第三种问题经常遇见。如何有效地避免局部最优的困扰？模拟退火算法应运而生。其实模拟退火也算是启发式算法的一种，具体学习的是冶金学中金属加热-冷却的过程。由S.Kirkpatrick, C.D.Gelatt和M.P.Vecchi在1983年所发明的，V.Čern在1985年也独立发明此演算法。
不过模拟退火算法到底是如何模拟金属退火的原理？主要是将热力学的理论套用到统计学上，将搜寻空间内每一点想象成空气内的分子；分子的能量，就是它本身的动能；而搜寻空间内的每一点，也像空气分子一样带有“能量”，以表示该点对命题的合适程度。演算法先以搜寻空间内一个任意点作起始：每一步先选择一个“邻居”，然后再计算从现有位置到达“邻居”的概率。若概率大于给定的阈值，则跳转到“邻居”；若概率较小，则停留在原位置不动。
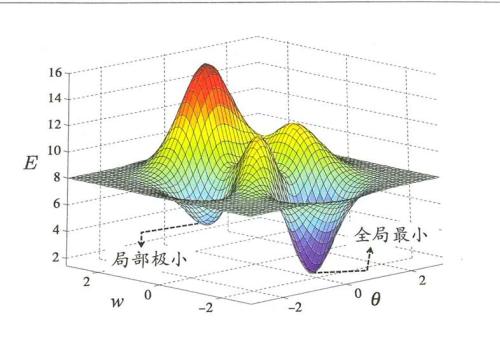
一、模拟退火算法基本思想
模拟退火是启发示算法的一种，也是一种贪心算法，但是它的搜索过程引入了随机因素。在迭代更新可行解时，以一定的概率来接受一个比当前解要差的解，因此有可能会跳出这个局部的最优解，达到全局的最优解。以下图为例，假定初始解为左边蓝色点A，模拟退火算法会快速搜索到局部最优解B，但在搜索到局部最优解后，不是就此结束，而是会以一定的概率接受到左边的移动。也许经过几次这样的不是局部最优的移动后会到达全局最优点D，于是就跳出了局部最小值。
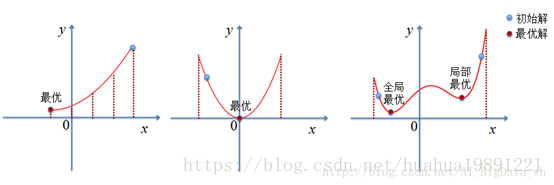
根据热力学的原理，在温度为时，出现能量差为dE的降温的概率为，表示为：
$p(dE)=exp(\frac{dE}{kT})$
其中是波尔兹曼常数，值为 $k=1.3806488\times10^{-23}$ ，exp表示自然指数，且。因此，所以函数的取值范围是(0, 1)。满足概率密度函数的定义。其实这条公式更直观意思就是：温度越高，出现一次能量差为的降温的概率就越大；温度越低，则出现降温的概率就越小。
在实际问题中，这里的“一定的概率”的计算参考了金属冶炼的退火过程。假定当前可行解为，迭代更新后的解为 $x_{new}$ ，那么对应的“能量差”定义为：
$\Delta f = f(x_{new}) - f(x)$
其对应的“一定概率”为：
最小值优化： $p(\Delta f)=exp(-\frac{\Delta f}{kT})$
最大值优化： $p(\Delta f)=exp(\frac{\Delta f}{kT})$
注：在实际问题中，可以设定，即将参数与合并。
二、模拟退火算法描述
初始化：初始温度（充分大），温度下限 $T_{min}$ （充分小），初始解状态（是算法迭代的起点），每个值的迭代次数；
对=1, 2, ..., 做第3至第6步；
产生新解 $x_{new}$ : $x_{new}=x+\Delta x$ ； $\Delta x$ 为 $[d_{min}, d_{max}]$ 之间的随机数。
利计算增量 $\Delta f = f(x_{new}) - f(x)$ ，其中为优化目标；
若 $\Delta f<0$ (若寻找最大值， $\Delta f>0$ )则接受 $x_{new}$ 作为新的当前解，否则以概率 $exp(-\Delta f / (kT))$ 接受 $x_{new}$ 作为新的当前解；
如果满足终止条件则输出当前解作为最优解，结束程序。(终止条件通常取为连续若干个新解都没有被接受时终止算法。)；
T逐渐减少，且 $T>T_{min}$ ，然后转第2步。
在每个温度下迭代次，通过不断改变x来寻找当前温度下的最优值，然后降低温度继续寻找，直到温度达到最低，即选择概率接近于0。

注意：生成新的后，要判断是否在定义域内，对于超出的值要抛弃。
三、模拟退火算法的优缺点
模拟退火算法的应用很广泛，可以高效地求解NP完全问题，如货郎担问题(Travelling Salesman Problem，简记为TSP)、最大截问题(Max Cut Problem)、0-1背包问题(Zero One Knapsack Problem)、图着色问题(Graph Colouring Problem)等等，但其参数难以控制，不能保证一次就收敛到最优值，一般需要多次尝试才能获得（大部分情况下还是会陷入局部最优值）。观察模拟退火算法的过程，发现其主要存在如下三个参数问题：
(1) 温度T的初始值设置问题
温度T的初始值设置是影响模拟退火算法全局搜索性能的重要因素之一、初始温度高，则搜索到全局最优解的可能性大，但因此要花费大量的计算时间；反之，则可节约计算时间，但全局搜索性能可能受到影响。
(2) 退火速度问题，即每个T值的迭代次数
模拟退火算法的全局搜索性能也与退火速度密切相关。一般来说，同一温度下的“充分”搜索是相当必要的，但这也需要计算时间。循环次数增加必定带来计算开销的增大。
(3) 温度管理问题
温度管理问题也是模拟退火算法难以处理的问题之一。实际应用中，由于必须考虑计算复杂度的切实可行性等问题，常采用如下所示的降温方式：
$T=\alpha \times T , \alpha \in (0, 1)$
注：为了保证较大的搜索空间，α一般取接近于1的值，如0.95、0.9

Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=694

©2021 上海优钧机械设备科技有限公司
沪ICP备19012247号-2

Best Last Month

农夫山泉港交所上市高开85.12% 总市值逾4400亿港元

农夫山泉港交所上市高开85.12% 总市值逾4400亿港元
Information industry

by wittx

RegNet

RegNet
Information industry

by wittx

LLM引擎把GPT-3调成ChatGPT

LLM引擎把GPT-3调成ChatGPT
Information industry

by wittx

新病毒担忧缓和欧美股市反弹

新病毒担忧缓和欧美股市反弹
Information industry

by wittx

公司上市的基本流程

公司上市的基本流程
Information industry

by wittx

AD模数转换

AD模数转换
Information industry

by wittx

房地产美元融资规模井喷

房地产美元融资规模井喷
Information industry

by wittx

辉瑞疫苗有效性 95% 称无严重不良反应

辉瑞疫苗有效性 95% 称无严重不良反应
Information industry

by wittx

2020/10/26 金融行情

2020/10/26 金融行情
Information industry

by wittx

风险模型

风险模型
Information industry

by wittx