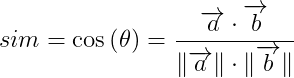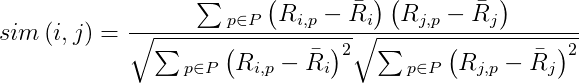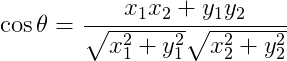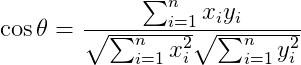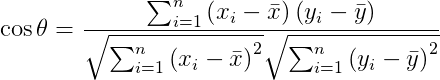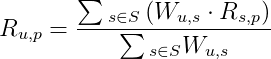协同过滤算法--Intelligent technology investment network-上海优钧机械设备科技

News Message

协同过滤算法

by show 2021-02-15

1 协同过滤

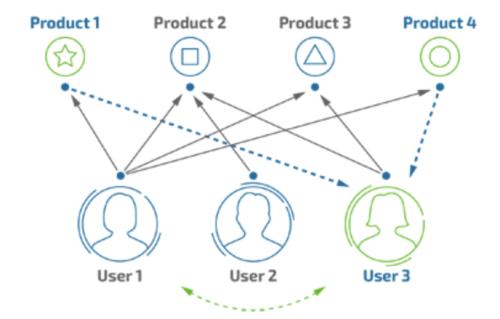
协同过滤就是协同别人的feedback，对信息进行过滤，从而选出某个用户可能感兴趣的信息。比如，某宝、某东的推荐页面，就是通过协同跟你自己相似用户的购买信息、评价和反馈，然后从所用商品中过滤出你可能感兴趣的东西推荐给你，简化的大致描述就是这样，可能会有出入，具体的详细算法流程后面会说。

推荐过程一共分为几个步骤：

获取所有物品的用户反馈，包括点赞、评价等等。
以上数据存储为矩阵形式，用户为行坐标，物品为列坐标，例如只统计点赞的数据，将点赞设为1，点踩设为-1，没有点赞或者点踩的设为0。这个矩阵被称为“共现矩阵”。
比如目标是预测用户c 对物品a 是否喜欢，由此就问题就转换为计算 (用户c , 物品a) 坐标上的数值，接近1就是喜欢，接近-1就是不喜欢。
计算每个用户跟目标用户的相似度，选出相似度最大的 Top 个用户，然后根据这个用户对目标商品的点赞情况，来预测目标用户对这个物品是否感兴趣。
如果预测接近1，则推荐；如果预测接近-1，则不推荐。

这是协同过滤算法的流程，但是其中模糊了几个点，比如如何计算用户的相似度，如何根据相似用户的feedback来计算目标用户的喜好程度，为什么以用户为行坐标，物品为列坐标构建共现矩阵等等，后面我会一一解释。

2 用户相似度计算

在协同过滤算法中，可通过上面的流程看出，相似度计算十分关键，他决定了具体选取哪些用户来确定目标用户的喜好程度。

2.1 余弦相似度

在共现矩阵中，所用行和列都可以做为一个向量，因此行向量也就是一个表示用户的向量，这个向量中包括了他对各种物品喜欢或者不喜欢的评价，所以这个向量可以看做是对用户的兴趣的一个描述。因为我们可以计算不同用户向量的夹角，夹角的大小用来表示两用户的相似程度。是用初中数学的知识我们可以得到如下公式：

$sim=\cos \left( \theta \right) =\frac{\overrightarrow{a}\cdot \overrightarrow{b}}{\lVert \overrightarrow{a} \rVert \cdot \lVert \overrightarrow{b} \rVert}$

2.2 Pearson相关系数

$sim\left( i,j \right) =\frac{\sum{_{p\in P}\left( R_{i,p}-\bar{R}_i \right) \left( R_{j,p}-\bar{R}_j \right)}}{\sqrt{\sum{_{p\in P}\left( R_{i,p}-\bar{R}_i \right) ^2}}\sqrt{\sum{_{p\in P}\left( R_{j,p}-\bar{R}_j \right) ^2}}}$

$R_{i,p}$ 代表用户对的评分， $\bar{R}_i$ 用户对所有物品的平均评分，代表所有的物品集合。

可以发现Pearson相关系数和余弦相似度都是分数形式，我们来对比一下两者之间的差别。

首先假设有两个向量， $\overrightarrow{a}=\left( x_1,y_1 \right)$ 、 $\overrightarrow{b}=\left( x_2,y_2 \right)$ ，将这两个向量带入余弦相似度的公式中，计算两向量的余弦相似度可以得到：

$\cos \theta =\frac{x_1x_2+y_1y_2}{\sqrt{x_{1}^{2}+y_{1}^{2}}\sqrt{x_{2}^{2}+y_{2}^{2}}}$

然后将两向量推广到高纬度， $\overrightarrow{a}=\left( x_1,x_2,x_3,x_4,... \right)$ 、 $\overrightarrow{b}=\left( y_1,y_2,y_3,y_4,... \right)$ ，再次计算余弦相似度可以得到：

$\cos \theta =\frac{\sum_{i=1}^n{x_iy_i}}{\sqrt{\sum_{i=1}^n{x_{i}^{2}}}\sqrt{\sum_{i=1}^n{y_{i}^{2}}}}$

此时可以发现，余弦相似度和Pearson相似度的公式形式十分相似了，只差一个均值。

令： $x'=\frac{x-\mu_x}{\sigma_y}$ ， $y'=\frac{y-\mu_y}{\sigma_y}$ ，将，带入上式中，可以得到：

$\cos \theta =\frac{\sum_{i=1}^n{\left( x_i-\bar{x} \right) \left( y_i-\bar{y} \right)}}{\sqrt{\sum_{i=1}^n{\left( x_i-\bar{x} \right) ^2}}\sqrt{\sum_{i=1}^n{\left( y_i-\bar{y} \right) ^2}}}$

观察发现这就是Pearson的公式了，其中， $x'=\frac{x-\mu}{\sigma}$ 是对x进行了正态分布的标准化操作。由此，余弦相似度和Pearson相似度就关联起来了。

我的想法：余弦相似度在对数据进行正态分布标准化之后就变成了Pearson相似度，因此在面对不同结构的数据的时候，对相似度计算方法的选择至关重要。而数据标准化的作用在于，可以将不同范围的数据映射到 [0,1] 这个范围内，或是将不同单位的数据无量纲化转化为纯数值，再或者在梯度下降时减少迭代次数以加快训练速度。举一个具体的例子，假如要求用户对商品进行打分，以用户对物品的打分构建共现矩阵。分值范围是0-100分，但是用户A习惯的打分区间是50-70分，而用户B的打分区间是80-100，假设用户AB真实的相似度极高，但是由于习惯的打分区间不同，这就会导致，两者的余弦夹角一定会存在一个相对来说较大的夹角，从而对相似度计算产生偏差，而标准化后，两者打分区间被映射到0-1这个区间里，则可以将这个夹角和真实的误差减小一些。同理，按照这个思路，用不同的数据标准化的方法是否可以推导出其他相似度计算的公式呢？

2.3 改良Pearson

基于Pearson相关系数，推导出了改良版的Pearson相关系数：

$sim\left( i,j \right) =\frac{\sum{_{p\in P}\left( R_{i,p}-\bar{R}_p \right) \left( R_{j,p}-\bar{R}_p \right)}}{\sqrt{\sum{_{p\in P}\left( R_{i,p}-\bar{R}_p \right) ^2}}\sqrt{\sum{_{p\in P}\left( R_{j,p}-\bar{R}_p \right) ^2}}}$

其中， $\bar{R_p}$ 代表物品p得到的所有评分中的总评分。

可以发现，改良版的Pearson相关系数的计算方法只是，把之前单个用户对所有物品的评分的平均分，改成了一个物品的所有评分的平均分。

这个做法同样可以以用我上面的例子解释，如果两个用户的打分区间不同，这样 $\bar{R_i}$ 和 $\bar{R_j}$ 不同，会使用户评分的偏置对标准化的结果造成较大影响，因此改用了单个物品的所有用户评分的均分。

我的想法：两向量标准化的尺度应该相同，这样标准化的结果和原始数据才具有更相似的结构。

因此，基于上面的上面的思想我们也可以构建不同的相似度计算方法，甚至是两向量差的模（我自己随便想的）说不定也可以作为相似度。

3 最终结果排序

在获得Top 相似用户之后，要利用Top 相似用户对目标用户进行推荐。首先要利用相似用户对商品已有的评价来对目标用户的喜好进行预测。预测方法常常使用加权平均：

$R_{u,p}=\frac{\sum{_{s\in S}}\left( W_{u,s}\cdot R_{s,p} \right)}{\sum{_{s\in S}W_{u,s}}}$

其中， $W_{u,s}$ 是用户和用户相似度的相似度， $R_{s,p}$ 是用户对物品的评分。这里比较容易理解。

获得用户对物品的评价的预测后，根据预测的得分进行排序，最中获得全部的排序列表。以上，就是协同过滤推荐的全过程。

以上的过程是基于用户相似度的协同过滤算法（UserCF），书中提到了两个缺点。

1. 用户数远大于物品数，这样在寻找Top 相似用户的时候，维护开销会过大，导致速度很慢，而且用户数量日益增长，导致用户相似度矩阵的存储所需空间几何倍增涨，难以存储。

2. 用户的历史数据往往非常稀疏，对于过于稀疏的用户，找到相似用户的准确度很低，导致UserCF不适用于那些购买频率低的物品。（这一点是我没有想到的）

4 ItemCF

由于UserDF算法的两点缺陷，ItemCF更常用，ItemCF与UserCF相对应，是基于物品相似度的协同过滤算法，根据物品列向量的相似度计算出物品之间的相似度矩阵，在找到用户的历史正反馈列表，将列表与物品相似度矩阵对比，选出Top 相似物品然后推荐。ItemCF算法具体流程如下：

1. 构建用户为行坐标（用户数为m），物品为列坐标（物品数为n）的m*n的共现矩阵。

2. 计算共现矩阵两两物品历史列向量之间的相似性，计算方法与用户相似度的计算方法相同，构建n*n的相似度矩阵。

3.获取用户的正反馈列表，然后对比相似度矩阵，选出和用户正反馈列表中的物品相似度高的并生成相似物品列表。

4.对相似列表里的物品根据相似度进行排序，然后生成推荐列表，如果一个物品与用户历史正反馈列表中多个物品相似，则这个物品的相似应为多个相似度相加。

5 UserCF和ItemCF对比

基于用户的推荐系统具有更强的社交性，比如某些app中可能感兴趣的人，脸书也有这个功能（个人感觉脸书这个朋友推荐很迷，不知道怎么做的，天天给我推荐一堆堆乱七八糟的人），对于某音，某头条这种推荐新闻或短视频的平台，UserCF更加适用，因为新闻兴趣点是分散的，相比用户对不同新闻的兴趣偏好，已经新闻及时性、热点性往往是更重要的属性，而UserCF适合发现热点，跟踪热点。（这里不是很理解。）

ItemCF更加适用于电商平台推荐，或者Netflix这种视频平台推荐，用户的兴趣点比较稳定，因此使用ItemCF更加合理。

Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=696