- Investment
- 科学论坛
-
Program
- Recruitment
- Center
News Message
电容器
- by wittx 2022-06-21
1. 孤立导体的电容
电容,顾名思义就是容纳电荷。如何定义电容这个物理量呢?
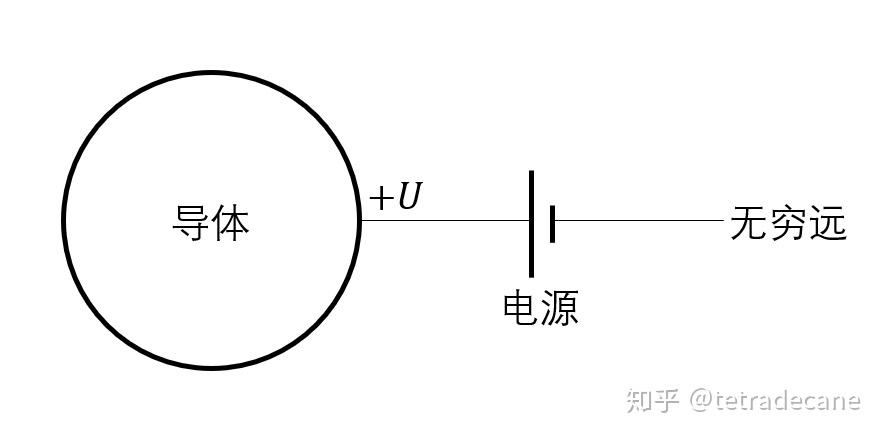
考虑一个在真空中的孤立导体球,并设无穷远点为零势能点。一开始,这个导体上没有电量,我们用一个电源来给它充电,电源的负极连接无穷远点,电源的正极连接该导体。如下图所示:
电池连导体 设电源的电压为
![[公式]](/images/download/1655808547779_22503.png) ,则导体的电势为
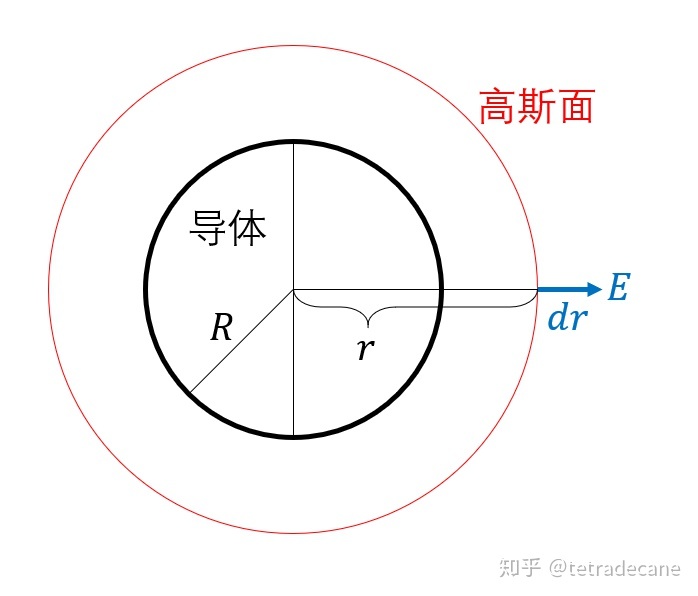
,则导体的电势为 ![[公式]](/images/download/1655808548263_79959.png) . 现在把电源撤去,导体上就带有了一定正电荷,电量是多少呢?需要用电场和电势来求解,如下图所示:
. 现在把电源撤去,导体上就带有了一定正电荷,电量是多少呢?需要用电场和电势来求解,如下图所示:求解导体的电量 设导体球半径为
![[公式]](/images/download/1655808548569_11724.png) ,带电
,带电 ![[公式]](/images/download/1655808548725_21263.png) ,根据静电场高斯定理,在距离球心
,根据静电场高斯定理,在距离球心 ![[公式]](/images/download/1655808548902_62792.png) 处的场强满足
处的场强满足![[公式]](/images/download/1655808549081_70355.png)
故
![[公式]](/images/download/1655808549251_65375.png) . 想象有一个带单位正电的试验电荷从该高斯面处背离圆心运动了距离
. 想象有一个带单位正电的试验电荷从该高斯面处背离圆心运动了距离 ![[公式]](/images/download/1655808549443_51506.png) ,那么电场力做功
,那么电场力做功 ![[公式]](/images/download/1655808549587_57529.png) ,电势(能)也就减小了
,电势(能)也就减小了 ![[公式]](/images/download/1655808549745_95376.png) . 因为导体是个等势体,想象从导体表面把试验电荷推到无穷远处,求得电势为
. 因为导体是个等势体,想象从导体表面把试验电荷推到无穷远处,求得电势为![[公式]](/images/download/1655808549865_59346.png)
因此导体带电
![[公式]](/images/download/1655808550093_38055.png) 与电源电压也即其电势
与电源电压也即其电势 ![[公式]](/images/download/1655808550236_29792.png) 成正比。
成正比。定义孤立导体的电容
![[公式]](/images/download/1655808550592_96345.png) ,其中
,其中 ![[公式]](/images/download/1655808550721_91341.png) 是该导体的带电量,
是该导体的带电量, ![[公式]](/images/download/1655808550891_92510.png) 是该导体的电势。电容单位为法(拉)(符号F, Farad),
是该导体的电势。电容单位为法(拉)(符号F, Farad), ![[公式]](/images/download/1655808551017_14993.png) . 孤立导体的电容与其形状、零势能点有关,与其带电量无关。
. 孤立导体的电容与其形状、零势能点有关,与其带电量无关。法拉是一个很大的电容单位,一个地球那么大的球形导体,其电容约为
![[公式]](/images/download/1655808551224_28058.png) . 因此,我们常用更小的单位,如微法、皮法。
. 因此,我们常用更小的单位,如微法、皮法。2. 电容器
2.1 电容器的电容
实际上很难有孤立的导体,导体周围总存在其它导体。把两个导体组合在一起,且互相绝缘,就可以称为电容器。
如果使两个导体分别带等量异号电荷
![[公式]](/images/download/1655808551382_42060.png) ,实验和理论均可证明,电量
,实验和理论均可证明,电量 ![[公式]](/images/download/1655808551549_96592.png) 与两个导体的电势差
与两个导体的电势差 ![[公式]](/images/download/1655808551666_77940.png) 成正比,定义电容器的电容
成正比,定义电容器的电容 ![[公式]](/images/download/1655808551816_54172.png) ,其中
,其中 ![[公式]](/images/download/1655808551975_10402.png) 只取正值,保证电容为正值。电容器的电容与其带电量、零势能点无关,只与电容器本身的构造有关。
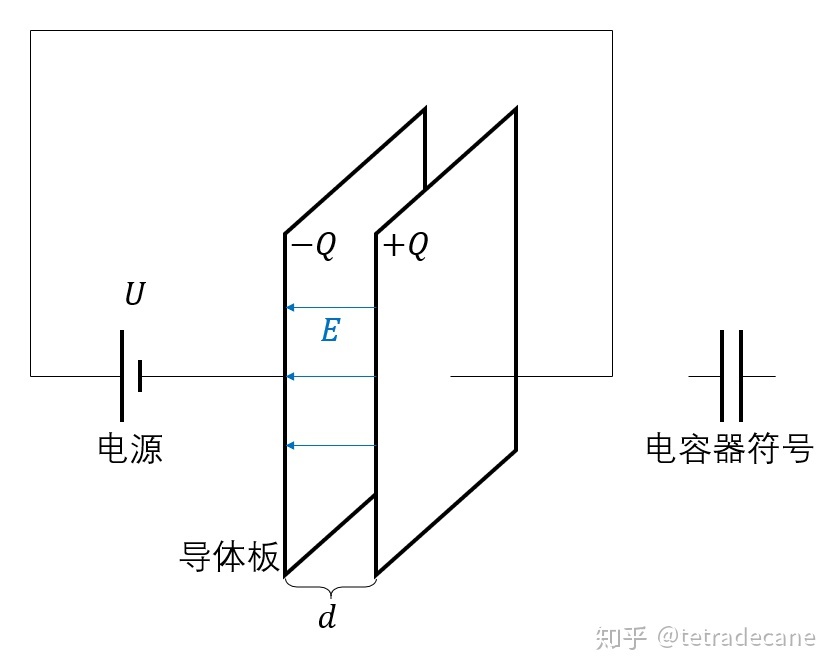
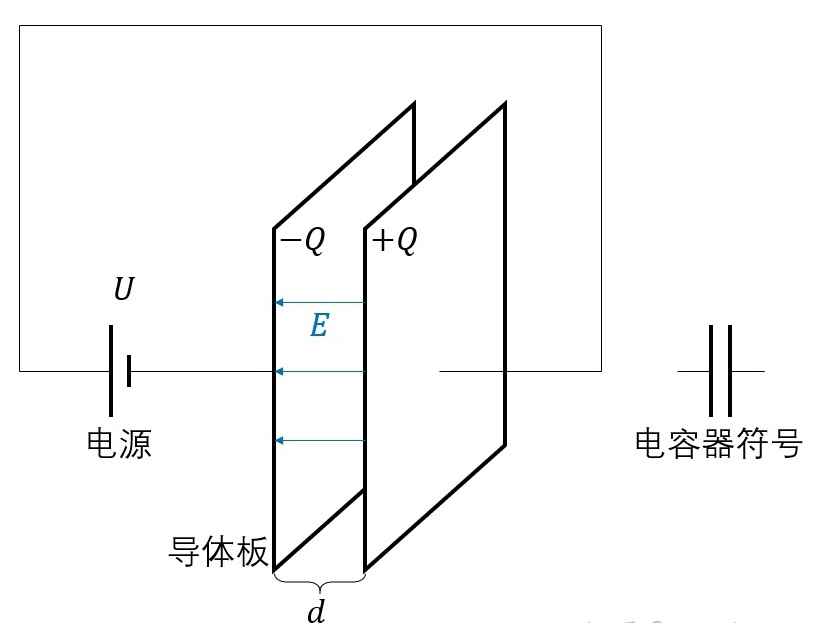
只取正值,保证电容为正值。电容器的电容与其带电量、零势能点无关,只与电容器本身的构造有关。最简单的电容器是平行板电容器,把两个相同大小的导体平板相对放置,分别引出导线,如下图所示:
平行板电容器 把这个电容器接上电压为
![[公式]](/images/download/1655808552208_92572.png) 的电源,则电容器两个极板上就会带电,产生电势差。一般的电路整体呈电中性,在稳定状态下,电容器两极板上带等量异号电荷。
的电源,则电容器两个极板上就会带电,产生电势差。一般的电路整体呈电中性,在稳定状态下,电容器两极板上带等量异号电荷。设电容器极板的面积为
![[公式]](/images/download/1655808552468_31780.png) ,相距
,相距 ![[公式]](/images/download/1655808552595_92521.png) ,两极板分别带电
,两极板分别带电 ![[公式]](/images/download/1655808552742_27345.png) . 因为
. 因为 ![[公式]](/images/download/1655808552881_44472.png) 一般很小,考虑两个极板之间的电场时,可以视极板为无穷大均匀带电平板,产生匀强电场
一般很小,考虑两个极板之间的电场时,可以视极板为无穷大均匀带电平板,产生匀强电场 ![[公式]](/images/download/1655808553017_96683.png) . 根据第1章静电场高斯定理最后的例子③,由于这里有两个匀强电场叠加,故
. 根据第1章静电场高斯定理最后的例子③,由于这里有两个匀强电场叠加,故![[公式]](/images/download/1655808553140_25009.png)
平行板电容器的电容,与极板面积
![[公式]](/images/download/1655808553444_56879.png) 成正比,与极板距离
成正比,与极板距离 ![[公式]](/images/download/1655808553589_64079.png) 成反比。电容器的符号也很形象地表示为上图右侧的那个符号。
成反比。电容器的符号也很形象地表示为上图右侧的那个符号。如果在平行板电容器中放入电介质,则其电容会发生变化。假设电介质的相对介电常数为
![[公式]](/images/download/1655808553827_40777.png) ,根据第4章静电场与电介质的2.3节的结论,在填充电介质之后,总电场
,根据第4章静电场与电介质的2.3节的结论,在填充电介质之后,总电场 ![[公式]](/images/download/1655808553952_59075.png) 不变,而导体板产生的外加电场变大为
不变,而导体板产生的外加电场变大为 ![[公式]](/images/download/1655808554208_61672.png) ,那么
,那么![[公式]](/images/download/1655808554342_89061.png)
电容也增大为原来的
![[公式]](/images/download/1655808554550_46352.png) 倍。因此,
倍。因此, ![[公式]](/images/download/1655808555014_39610.png) 又称为电容率。
又称为电容率。我们希望造出比较大的电容,用一个电压不大的电源给它充电时,也能存比较多的电量。平行板电容器增大电容,有两种途径:
- 一种途径是减小极板距离。但是,极板距离不能太小,否则它们之间的电介质太薄,容易被击穿而导电。电容器是最怕击穿的,击穿之后它就变成了导线,不能容电且不可逆,相当于废了,甚至有受热膨胀而爆炸的可能。也正是因此,电容器所受电压有限额,不允许超出。
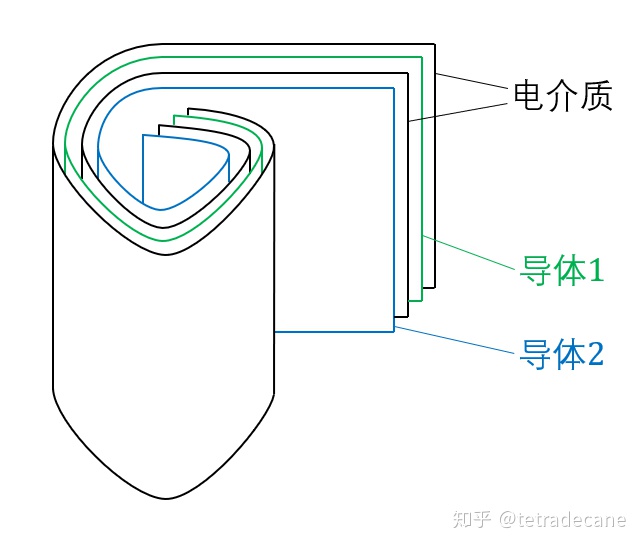
- 另一种途径是增大极板面积。但是,大的板子很占地。因此,人们发明了一种增大极板面积的方式,如下图所示:
卷绕型电容器 一层电介质,一层导体1,一层电介质,一层导体2,这么铺4层,然后卷绕起来。两种导体之间没有短路,接触面积也比较大,因此电容也比较大。
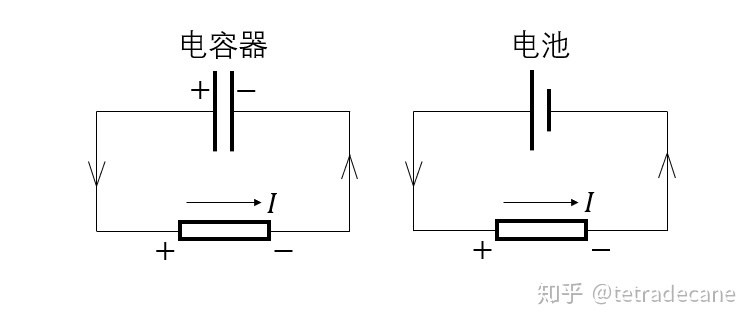
电容充好电后,就可以当一个“电池”用,可以给用电器供电,如下图所示:
电容与电池的放电 电容器会给电阻供电,电阻发热,电能转化为热能。等到电容器的电荷量被中和完毕时,电能也就全部消耗了。
电容和电池有什么区别?①原理上来说,电容存储的是真真实实的电荷,存储的是电能;电池内部是一堆化学原料,存储的是化学能,电池放电时是化学能转化为电能。电池有个更形象的名称叫做“电泵”(暂不考虑充电),而电容器则相当于“电库”。②优缺点来说,电容放电时电压不稳定,而且存的电比较少,但是充放电很快。上图左称作RC电路,在电路学中可用微分方程解出,电容的电压是指数级趋近于0的(此处不予证明);而电池的化学能匀速转化,电压在相当长的时间内比较稳定。相同体积下,一般电池比电容容量大得多,充电也慢得多。
2.2 电容器的串并联
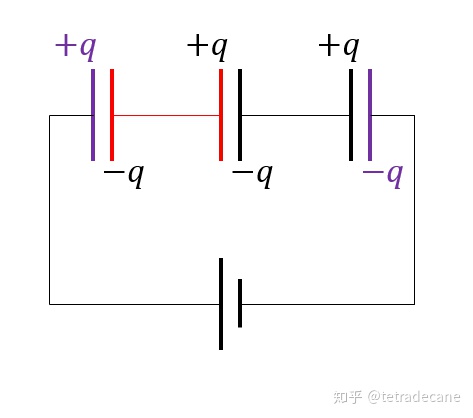
①电容器串联时如下图所示:
电容器串联 设第一个电容器的左极板带电
![[公式]](/images/download/1655808555279_50256.png) ,那么其右极板带电
,那么其右极板带电 ![[公式]](/images/download/1655808555404_28811.png) . 由于红色部分呈电中性,故第二个电容器的左极板也带电
. 由于红色部分呈电中性,故第二个电容器的左极板也带电 ![[公式]](/images/download/1655808555523_66195.png) ,以此类推得到每个电容器每个极板的电量都是
,以此类推得到每个电容器每个极板的电量都是 ![[公式]](/images/download/1655808555682_55172.png) .
.设三个电容器的电容分别为
![[公式]](/images/download/1655808555820_23216.png) ,则它们的电压分别为
,则它们的电压分别为 ![[公式]](/images/download/1655808556011_76110.png) ,电源电压为
,电源电压为 ![[公式]](/images/download/1655808556162_99749.png) . 把这三个电容器等效为一个电容器,其电荷相当于两个紫色极板上的电荷(其余极板绝缘于电源,与等效电容无关),因此等效电容为
. 把这三个电容器等效为一个电容器,其电荷相当于两个紫色极板上的电荷(其余极板绝缘于电源,与等效电容无关),因此等效电容为![[公式]](/images/download/1655808556344_43730.png)
也就是说,等效电容的倒数,等于所有串联电容的倒数之和。电容越串联越小。
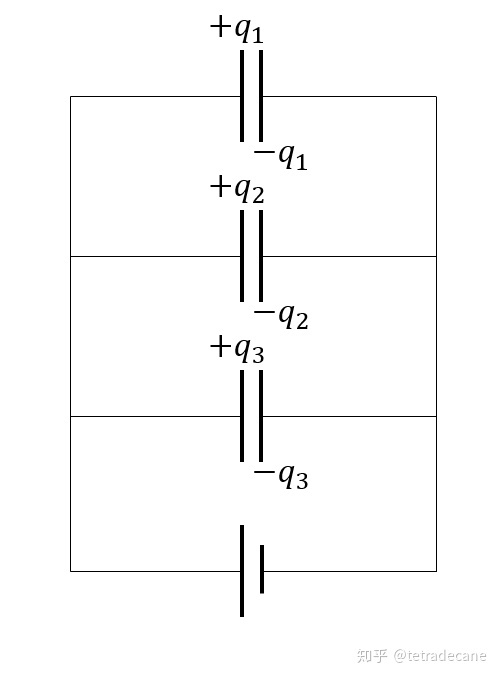
②电容器并联时如下图所示:
电容器并联 设电源电压为
![[公式]](/images/download/1655808556534_82480.png) ,那么每个电容器上的电压都为
,那么每个电容器上的电压都为 ![[公式]](/images/download/1655808556698_18159.png) .
.设三个电容器的电容分别为
![[公式]](/images/download/1655808556975_52755.png) ,则它们的电量分别为
,则它们的电量分别为 ![[公式]](/images/download/1655808557105_70942.png) . 把这三个电容器等效为一个电容器,其电荷量相当于三个电容器之和,因此等效电容为
. 把这三个电容器等效为一个电容器,其电荷量相当于三个电容器之和,因此等效电容为![[公式]](/images/download/1655808557318_61318.png)
也就是说,等效电容等于所有并联电容之和。电容越并联越大。
3. 静电场的能量
3.1 带电体系的静电能
设有一个带电体系,我们定义一个量,以概括这个体系因静电场而存在的能量。定义无穷远处为零势能点,把带电体系内的所有电荷都推向无穷远处,则它们之间不再有相互作用的电场力,成为“自由状态”,称这个过程中电场力做的总功为这个带电体系的静电能
![[公式]](/images/download/1655808557497_89949.png) .
.按上述定义,如果带电体系只有两个同号电荷,则静电能为正值;如果带电体系只有两个异号电荷,则静电能为负值。
设带电体系仅有两个电荷
![[公式]](/images/download/1655808557683_86335.png) . 先视
. 先视 ![[公式]](/images/download/1655808557826_17864.png) 为场源电荷,把
为场源电荷,把 ![[公式]](/images/download/1655808558052_32442.png) 推向无穷远处,考虑
推向无穷远处,考虑 ![[公式]](/images/download/1655808558188_70550.png) 的电势为
的电势为 ![[公式]](/images/download/1655808558334_13622.png) ,则静电能为
,则静电能为 ![[公式]](/images/download/1655808558460_27071.png) ;同理,视
;同理,视 ![[公式]](/images/download/1655808558668_79239.png) 为场源电荷,把
为场源电荷,把 ![[公式]](/images/download/1655808558792_48276.png) 推向无穷远处时,静电能为
推向无穷远处时,静电能为 ![[公式]](/images/download/1655808558962_86963.png) . 可以把静电能综合写成对称的形式:
. 可以把静电能综合写成对称的形式: ![[公式]](/images/download/1655808559103_69051.png) .
.设带电体系仅有三个电荷
![[公式]](/images/download/1655808559289_48880.png) . 记
. 记 ![[公式]](/images/download/1655808559421_14723.png) 表示仅以
表示仅以 ![[公式]](/images/download/1655808559606_37168.png) 为场源电荷时,
为场源电荷时, ![[公式]](/images/download/1655808559742_84676.png) 的电势,则
的电势,则 ![[公式]](/images/download/1655808559890_79534.png) 与
与 ![[公式]](/images/download/1655808560021_12158.png) 的互能(相互间的静电能)为
的互能(相互间的静电能)为 ![[公式]](/images/download/1655808560201_53341.png) ,
, ![[公式]](/images/download/1655808560646_75513.png) 与
与 ![[公式]](/images/download/1655808560820_39938.png) 的互能为
的互能为 ![[公式]](/images/download/1655808560948_54098.png) ,
, ![[公式]](/images/download/1655808561234_66254.png) 与
与 ![[公式]](/images/download/1655808561361_19335.png) 的互能为
的互能为 ![[公式]](/images/download/1655808561530_70886.png) ,那么整个体系的静电能为上面三式子求和:
,那么整个体系的静电能为上面三式子求和:![[公式]](/images/download/1655808561677_74308.png)
由于电势可以直接叠加,记
![[公式]](/images/download/1655808561902_53635.png) 表示除了电荷
表示除了电荷 ![[公式]](/images/download/1655808562037_61932.png) 之外,其他所有电荷作为场源电荷时,
之外,其他所有电荷作为场源电荷时, ![[公式]](/images/download/1655808562240_65277.png) 的电势,那么
的电势,那么![[公式]](/images/download/1655808562731_73730.png)
类似可证明,任意n个点电荷构成的带电体系的静电能也为
![[公式]](/images/download/1655808562916_82939.png) .
.对于连续带电体,用微元法类似分析,可得到
![[公式]](/images/download/1655808563077_46988.png) ,其中
,其中 ![[公式]](/images/download/1655808563247_33170.png) 原则上表示除去电荷元
原则上表示除去电荷元 ![[公式]](/images/download/1655808563448_34492.png) 之外其他所有电荷作为场源电荷时
之外其他所有电荷作为场源电荷时 ![[公式]](/images/download/1655808563612_72192.png) 的电势,但实际上可以将
的电势,但实际上可以将 ![[公式]](/images/download/1655808563836_86871.png) 视为所有电荷作为场源电荷时
视为所有电荷作为场源电荷时 ![[公式]](/images/download/1655808563993_31004.png) 处的电势
处的电势 ![[公式]](/images/download/1655808564117_35060.png) ,因为
,因为 ![[公式]](/images/download/1655808564241_22291.png) 为
为 ![[公式]](/images/download/1655808564361_18467.png) 的一阶无穷小,再乘以
的一阶无穷小,再乘以 ![[公式]](/images/download/1655808564546_19595.png) 即为二阶无穷小,积分之后是一阶无穷小,可以忽略。
即为二阶无穷小,积分之后是一阶无穷小,可以忽略。带电体系的静电能 3.2 电容器的静电能
对于电容器,其静电能很容易计算。设两个极板分别带电
![[公式]](/images/download/1655808564731_44806.png) ,其中负电极板接地,则正电极板的电势为
,其中负电极板接地,则正电极板的电势为 ![[公式]](/images/download/1655808564874_79874.png) ,那么该电容器所带的静电能就为
,那么该电容器所带的静电能就为![[公式]](/images/download/1655808565038_83809.png)
还有另一种推导平行板电容器的静电能的方法。前面提到,一个带电体系的静电能就是所有电荷都推向无穷远处时,电场力做的总功。无穷远处和接地的负极板等电势,所以静电能也等于把正极板推向负极板并合二为一时,电场力做的总功。负极板带电
![[公式]](/images/download/1655808565383_70262.png) ,产生的匀强电场大小为
,产生的匀强电场大小为 ![[公式]](/images/download/1655808565555_17778.png) (只考虑一个极板,所以要除以2),给予正极板恒定的电场力
(只考虑一个极板,所以要除以2),给予正极板恒定的电场力 ![[公式]](/images/download/1655808565689_75737.png) ,两极板合二为一时电场力做功
,两极板合二为一时电场力做功![[公式]](/images/download/1655808565845_77938.png)
与上述结论一致。
3.3 静电场的能量密度
在某些场景下(如集成电路中),我们希望电容器的体积尽可能小,而让它存储的静电能尽可能多。因此,单位体积的静电能是值得研究的,称其为静电场的能量密度
![[公式]](/images/download/1655808566112_76564.png) ,单位为
,单位为 ![[公式]](/images/download/1655808566276_68225.png) .
.设平行板电容器内部充满绝对介电常数为
![[公式]](/images/download/1655808566495_11236.png) 的电介质,则
的电介质,则![[公式]](/images/download/1655808566667_84688.png) 且
且 ![[公式]](/images/download/1655808566843_43100.png)
![[公式]](/images/download/1655808567032_84212.png)
注意这里的
![[公式]](/images/download/1655808567249_67399.png) 正好表示电容器的体积,那么其能量密度为
正好表示电容器的体积,那么其能量密度为![[公式]](/images/download/1655808567427_92456.png)
根据
![[公式]](/images/download/1655808567562_79679.png) ,静电场能量密度还可以写为
,静电场能量密度还可以写为![[公式]](/images/download/1655808567748_81143.png)
实际上,这个结论也适用于非匀强电场,任何一点的能量密度也为
![[公式]](/images/download/1655808567916_43239.png) ,那么对能量密度进行积分,也能得到整个带电体系的静电能,即
,那么对能量密度进行积分,也能得到整个带电体系的静电能,即![[公式]](/images/download/1655808568131_75075.png)
总结
孤立导体的电容
![[公式]](/images/download/1655808568298_75710.png) ,单位为
,单位为 ![[公式]](/images/download/1655808568473_76711.png) .
.电容器的电容
![[公式]](/images/download/1655808568596_83478.png) (定义式),平行板电容器的电容
(定义式),平行板电容器的电容 ![[公式]](/images/download/1655808568778_30585.png) (决定式)。
(决定式)。电容器较电池,具有容量较小、充放电快的特点,直接存储静电能。
电容器串联
![[公式]](/images/download/1655808568998_87316.png) ,电容器并联
,电容器并联 ![[公式]](/images/download/1655808569226_46385.png) .
.点电荷系的静电能
![[公式]](/images/download/1655808569367_64131.png) ,其中
,其中 ![[公式]](/images/download/1655808569568_70755.png) 表示除了电荷
表示除了电荷 ![[公式]](/images/download/1655808569706_53213.png) 之外,其他所有电荷作为场源电荷时,
之外,其他所有电荷作为场源电荷时, ![[公式]](/images/download/1655808569826_66672.png) 的电势。
的电势。连续带电体系的静电能
![[公式]](/images/download/1655808569971_82043.png)
![[公式]](/images/download/1655808570169_21028.png)
其中
![[公式]](/images/download/1655808570344_96881.png) 表示静电场的能量密度,即单位体积的能量,
表示静电场的能量密度,即单位体积的能量, ![[公式]](/images/download/1655808570516_66529.png) .
.
Share Http URL: http://www.wittx.cn/get_news_message.do?new_id=961
Best Last Month
Information industry by wittx

Information industry by wittx
Information industry by wittx
Information industry by wittx
Information industry by wittxVortex field simulation and analysis of a solar updraft power engine
Information industry by wittx

Information industry by wittx

Petrochemical industry by wittxLarge-area and adaptable electrospun silicon-based thermoelectric nanomaterials with high energy con

Information industry by wittx

Information industry by wittx